Two’s Complement: What is It and How to Find It?

There are just two digits, 0 and 1, in the binary system. There is no explicit way to indicate the negativity of a number in this system. Two’s complement is a mathematical technique that allows us to represent negative numbers using binary digits. This method is widely used in computer systems and digital arithmetic to perform operations with both positive and negative integers.

In this article, we will delve into the concept of two’s complement, which is an essential technique for representing and manipulating negative binary numbers. We will provide many examples to make it easy to understand for our readers.

What is Two’s Complement? 

It is a numerical system used in computer arithmetic to represent both positive and negative numbers. It works by taking the binary representation of the positive number and inverting all the bits, then adding 1.

This system assigns the most significant bit (the leftmost bit) as the sign bit, with 0 representing a positive number and 1 representing a negative number. All the other bits in the number represent the magnitude. Two’s Complement facilitates the addition and subtraction of negative numbers without the need for additional circuitry or sign detection algorithms.

How to Find the Two’s Complement?

The two’s complement of a binary number can be obtained by following steps:

1. Convert the given numbers into a binary numbers system. Move to the next step if the given number is already in binary form.
2. Flip all the bits (change 0s to 1s and vice versa).
3. Add 1 to the flipped number.

Example:

Find the two’s (2’s) complements of the binary number 1101.

Solution:

Invert the bits: 0010

Add 1: 0011

Thus, the two’s complement of 1101 is 0011.

Alternative Method to Find 2’s Complement

Here is a second method to find 2’s complement:

1. Convert the given number to its binary representation. If the number is already in binary format, move on to the next step.
2. Identify the rightmost ‘1’ in the binary representation.
3. Leave this ‘1’ unchanged and invert (flip) all digits to the left of it.

Example: The binary representation of the positive number 9 is 1001. The rightmost ‘1’ is in the 1^st position from the right. We leave this ‘1’ unchanged and invert the remaining left bits, giving us 0111, which is the two’s complement of 9.

Subtraction Using Two’s Complement

Subtracting binary numbers using 2’s complement involves the following steps:

1. Take the two’s complement of the subtrahend.
2. Add the two’s complement of the subtrahend to the minuend.
3. If the result does not produce a carry, take the two’s complements of the result. It will be a negative number.
4. If the result produces a carry bit of 1, discard the carry bit. There will be a positive number as a result.

Example:

Subtract 00101 from 10101.

Solution:

Calculate the 2’s complement of the subtrahend, which is 11011. Then, perform the addition: 10101 + 11011 = 1 10000. Since there is a carry bit (1) in the result, discard the carry bit, and the result is 10000, which is a positive number.

Addition using two’s complement:

Here are the three different cases of addition using two’s complement:

CASE-1: Adding positive and negative numbers when a positive number is greater than a negative number

1. Find 2’s complement of the negative number.
2. Add the positive and 2’s complement of the negative number.
3. Ignore any carry bit.
4. There will be a positive number as a result.

CASE-2: Adding positive and negative numbers when the negative number is greater than the positive number

1. Convert the negative number into its two’s complement.
2. Add the positive and 2’s complement of the negative number.
3. Do not consider an end-around carry bit.
4. Change the result back to 2’s complement form.
5. There will be a negative number as a result.

CASE-3: Sum of Two Negative Numbers

1. Convert both negative numbers into their respective two’s complement forms.
2. Add them, dropping the carry bit.
3. Take the 2’s complements of the previous result.
4. The final two’s complement expresses the addition of two negative numbers.

Two’s Complement Advantages

Two’s complement offers several advantages over other methods of representing negative numbers:

• Two’s complement simplifies arithmetic operations
• It provides a consistent representation of both positive and negative numbers
• Most computer hardware is designed to work with two complements
• Subtracting two binary numbers is simplified when both numbers are in two’s complement form.
• Two’s complement can detect overflow errors, which can occur when the result of an arithmetic operation is too large to be represented within the given number of bits.

Examples of Two’s Complement

Let’s illustrate how to find two’s complement with the help of some examples.

Example 1.

Find the two’s complements of the decimal number 25 in 8-bit.  

2	25
2	12 – 1
2	6 – 0
2	3 – 0
	1 – 1

Solution:

The binary representation of 25 = 11001

Bits chosen for this example = 8

25 in binary form after completing 08 bits = 00011001

Flip all the 0s to 1s and all the 1s to 0s of the binary number 00011001. i.e. 11100110             

Add 1 in a flipped binary number system.

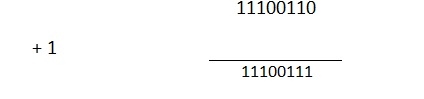
Thus, two’s complements of the decimal number 25 with an 8-selected bitis1110 0111. 

You can also use a two’s complement calculator to deal the challenges of converting numbers into 2’s complement.

Example 2.

Add -1100 and 0011

Solution:

Take the Two’s complement of 1100.

Flip all 0s to 1s and vice versa. 1100 à 0011

Add 1 in 0011. i.e. (0011 + 1 = 0100)

2’s complement of 1100 is 0100.

Add 0100 and 0011.

       

Thus, the Sum of -1100 and 0011 is 0111.

Conclusion:

In this article, we have explored Two’s Complement, which is a crucial numerical system in computer arithmetic for representing positive and negative binary numbers. We learned two different methods to find out 2’s complement with examples. We discussed how to add or subtract by using two’s complement. Understanding it is essential in digital electronics and computing.