NCERT Solutions For Class 9 Mathematics | Linear Equations In Two Variables | Chapter 4 Exercise 4.3
1. Draw the graph of each of the following linear equations in two variables:
i) x + y = 4
ii) x – y = 2
iii) y = 3x
iv) 3 = 2x + y
Answer:
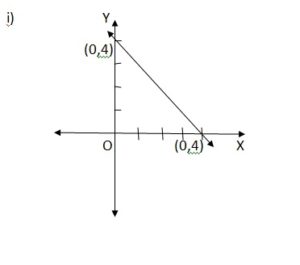
Given equation is x + y = 4
We need to find the two points.
When x = 0, y = 4
When y= 4, x = 4 – y = 4 – 4 = 0
Therefore, two points are (0, 4) and (4, 0).
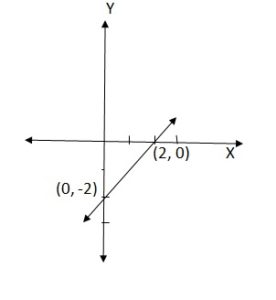
Given equation is x – y =2
When x = 2, 2 – y = 2 then y= 0
When x = 0, 0 – y = 2 then y = -2
Therefore, two points are (2, 0) and (0,-2).
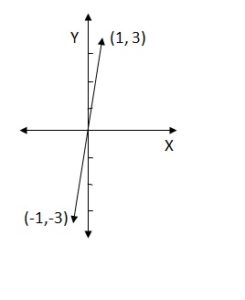
Given equation is y = 3x
When x =1, y = 3
When x = -1, y = -3
Therefore, the two points are (1, 3) and (-1,-3).
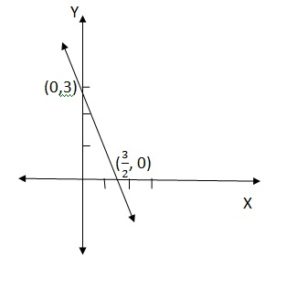
Given equation is 3 = 2x + y
When x = 0, 3 = 2×0 + y then y =3
When y = 0, 3 = 2x + 0 then x =3/2.
Therefore, the two points are (0, 3) and (3/2, 0).
2. Give the equations of two lines passing through (2, 14). How many more such lines are there and why?
Answer:
When x= 2 and y= 14, one equation is x + y = 2 + 14 = 16
Another equation is y = 7x or 7x – y = 0
Therefore, 7x – y = 0 and x + y = 16 are the two equations of two lines passing through (2, 14).
Infinitely many such lines are there, because through a point infinitely many lines can be drawn.
3. If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a?
Answer:
Given 3y = ax + 7
If the point (3, 4) lies on the graph of the equation 3y = ax +7,
we can take x =3 and y = 4.
Then, 3 (4) = a (3) +7
12 = 3a + 7
3a = 12 – 7= 5
a = 5/3.
4. The taxi fare in a city is as follows: For the first kilometre, the fare is Rs 8 and for the subsequent distance it is Rs 5 per km. Taking the distance covered as x km and total fare as Rs y, write a linear equation for this information, and draw its graph.
Answer:
Take the distance covered = x km and total fare = Rs y.
Fare for the first kilometer = Rs 8
Fare for the subsequent distance = Rs 5
Fare for the rest of the distance = Rs (x-1) 5
The linear equation for this information is given by,
y = 8 + (x -1)5
y = 8 + 5x – 5
y = 3 + 5x
5x – y +3 =0
When x = 0, y = 3
When x = 1, y = 3 + 5 x 1 = 8
Therefore, the two points are (0, 3) and (1, 8).